02 Feb 2014
诈金花各类别牌的概率分布:统计的方法
过年,诈金花游戏
大年初三,走亲访戚。弟弟女朋友到家串门,4人一起玩诈金花游戏打发时间。一连玩了好几把,没有赢过一次,全当陪练了:连对子都没来过。我好奇了,
- 抓到各类牌的概率是多少?
- 怎么样最大化赢的概率:在已知自己的牌,以及对方的出价的前提下,是应该跟/弃/加价?
第一个问题是第二个的基础。每次选择都是一种冒险(除非手握3张A,这时需要的是诱导),但需要努力做到是caculated risk。
相信是可以通过数学计算得出各类牌的概率。但对于我这样一个可以通过程序来奴役机器的程序员来说,另外一个自然的想法:让机器随机发牌,通过统计,来估算各类牌出现的概率,当样本空间足够大,统计结果会逼近理论值。
结论
每次发4个人的牌,随机发10万次,统计40万副牌中,各类的概率分布: 
一个意外的有趣发现,牌面上,同花色比顺子大,但出现概率上,顺子更小。同样的还有同花顺和3同牌。
计算了德州扑克的概率分布:它的9种类别的牌的概率,严格按照递增顺序。似乎设计诈金花的人,概率差一点。德州扑克也更好玩:未来的不确定性,以及博弈。
在n人的游戏中,发n副牌,最大的一副牌的类别的概率分布:
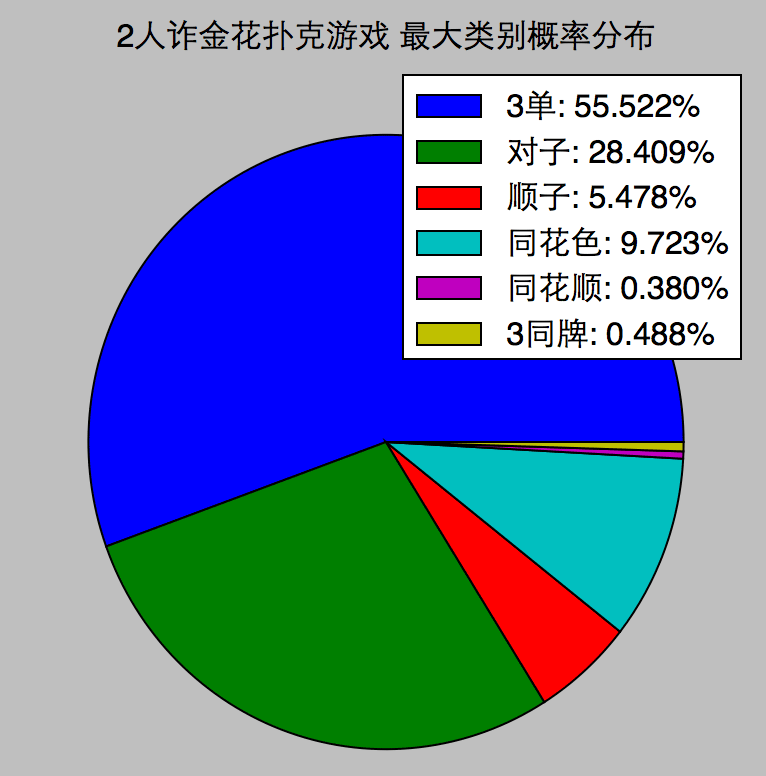

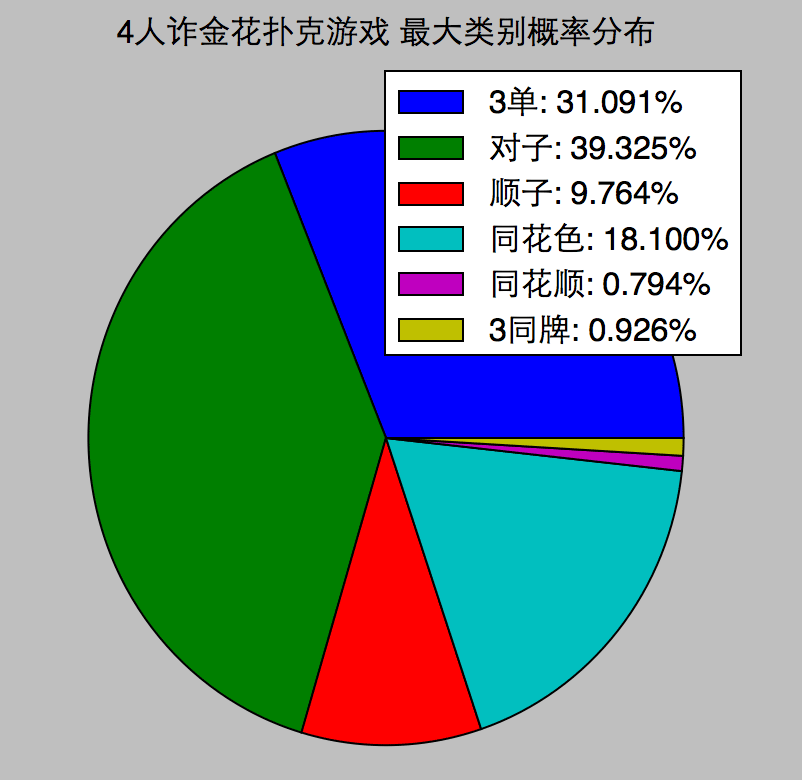
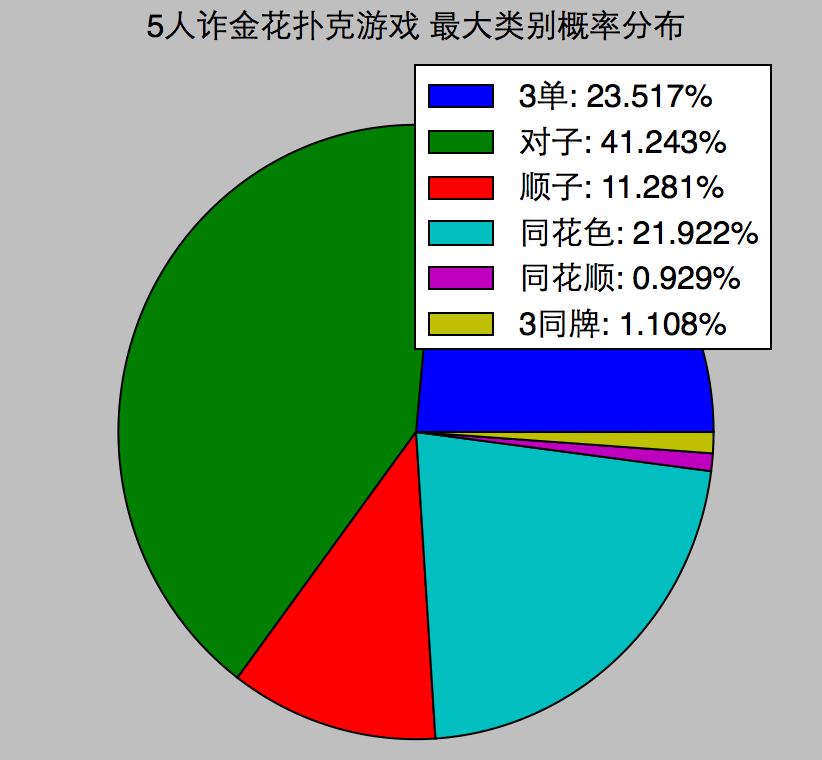

code
发牌:一副牌,先洗牌,再从中抽出numhands份,各n张牌
def deal(numhands, n=5, deck=[i + s for i in '23456789TJQKA' for s in "SHDC"]):
"Shuffle the deck and deal out numhands n-card hands"
random.shuffle(deck)
return [deck[n * i:n * (i + 1)] for i in range(numhands)]计算牌面类别
def jinhua_rank(hand):
groups = group(["--23456789TJQKA".index(r) for r, s in hand])
counts, ranks = unzip(groups)
ranks = sorted(ranks, reverse=True)
straight = len(set(ranks)) == 3 and (max(ranks) - min(ranks) == 2) # 顺子
flush = len(set([s for r, s in hand])) == 1 # 同花
if counts == (3, ): # 3各牌,一样
return 8, max(ranks)
elif straight and flush: # 同花顺
return 7, max(ranks)
elif flush: # 同花
return 6, ranks
elif straight: # 顺子
return 5, max(ranks)
elif counts == (2, 1): # 一对
return 4, kind(2, ranks), ranks
else: # 3单
return 3, ranks辅助函数
def group(items):
groups = [(items.count(x), x) for x in set(items)]
groups.sort(reverse=True)
return groups
def unzip(pairs): return zip(*pairs)